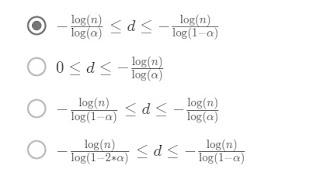In this article i am gone to share Coursera Course Divide and Conquer, Sorting and Searching, and Randomized Algorithms Week 3 | Problem Set #3 Quiz Answer with you..

Divide and Conquer, Sorting and
Searching, and Randomized Algorithms

Also visit this link:  Problem Set #2 Quiz Answer

Problem Set #3 Quiz Answer

Question 1) Let 0 < a <.5 be some constant (independent of the input array length n). Recall the Partition subroutine employed by the QuickSort algorithm, as explained in lecture. What is the probability that, with a randomly chosen pivot element, the Partition subroutine produces a split in which the size of the smaller of the two subarrays is ≥ a times the size of the original array?

• 1 – 2 ✲ a
• a
• 1 – a
• 2 – 2✲a

Question 2) Now assume that you achieve the approximately balanced splits above in every recursive call —that is, assume that whenever a recursive call is given an array of length k, then each of its two recursive calls is passed a subarray with length between ak and (1 – a)k (where a is a fixed constant strictly between 0 and.5). How many recursive calls can occur before you hit the base case? Equivalently, which levels of the recursion tree can contain leaves? Express your answer as a range of possible numbers d, from the minimum to the maximum number of recursive calls that might be needed.

Question 3) Define the recursion depth of QuickSort to be the maximum number of successive recursive calls before it hits the base case — equivalently, the number of the last level of the corresponding recursion tree. Note that the recursion depth is a random variable, which depends on which pivots get chosen. What is the minimum-possible and maximum-possible recursion depth of QuickSort, respectively?

• Minimum: Θ(log(n)); Maximum: Θ(n)
• Minimum: Θ(log(n)); Maximum: Θ(n log(n))
• Minimum: Θ(1); Maximum: Θ(n)
• Minimum: Θ(√n); Maximum: Θ(n)

Question 4) Consider a group of k people. Assume that each person’s birthday is drawn uniformly at random from the 365 possibilities. (And ignore leap years.) What is the smallest value of k such that the expected number of pairs of distinct people with the same birthday is at least one?

[Hint: define an indicator random variable for each ordered pair of people. Use linearity of expectation.]

• 28
• 27
• 20
• 23
• 366

Question 5) Let X1, X2, X3 denote the outcomes of three rolls of a six-sided die. (l.e., each Xi  is uniformly distributed among 1,2,3,4,5,6, and by assumption they are independent.) Let Y denote the product of X1 and X2 and Z the product of X2 and X3. Which of the following statements is correct?

• Y and Z are independent, but E[Y ✱ Z] ≠ E[Y]✱ E[Z].
• Y and Z are independent, and E[Y ✱ Z] ≠ E(Y] ✱ E[Z].
• Y and Z are not independent, and E[Y ✱ Z] ≠ E(Y] ✱ E[Z].
• Y and Z are not independent, but E[Y ✱ Z] ≠ E(Y] ✱ E[Z].