All Coursera Quiz Answers

Applied Machine Learning in Python Module 3 Quiz Answer

by Niyander

Hello Friends in this article i am gone to share Applied Machine Learning in Python Coursera Module 3 Quiz Answers with you..

Applied Machine Learning in Python Quiz Answer

Also visit this link:  Applied Machine Learning in Python Module 2 Quiz Answer

 

Question 1) A supervised learning model has been built to predict whether someone is infected with a new strain of a virus. The probability of any one person having the virus is 1%. Using accuracy as a metric, what would be a good choice for a baseline accuracy score that the new model would want to outperform?

  • 0.99

 

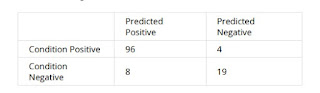
Question 2) Given the following confusion matrix:

Applied Machine Learning in Python Module 3 Quiz Answer

Compute the accuracy to three decimal places.

  • 0.906
 

Question 3) Given the following confusion matrix:

Applied Machine Learning in Python Module 3 Quiz Answer
Compute the precision to three decimal places. 
  • 0.923 
 

Question 4) Given the following confusion matrix:

Applied Machine Learning in Python Module 3 Quiz Answer
Compute the precision to three decimal places. 
  • 0.960

Question 5) Using the fitted model `m` create a precision-recall curve to answer the following question:

For the fitted model `m`, approximately what precision can we expect for a recall of 0.8?
(Use y_test and X_test to compute the precision-recall curve. If you wish to view a plot, you can use `plt.show()` )
  1. #print(m)
  2. pre,rec,_ = precision_recall_curve(y_test,m.predict(X_test))
  3. plt.plot(rec,pre)
  4. plt.xlabel(‘Recall’)
  5. plt.ylabel(‘Precision’)
  6. plt.ylim([0.0, 1.05])
  7. plt.xlim([0.0, 1.0])
  8. plt.show()
 
  • 0.6

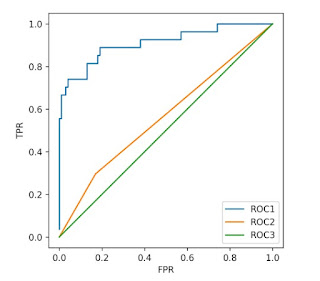
Question 6)Given the following models and AUC scores, match each model to its corresponding ROC curve.

• Model 1 test set AUC score: 0.91
• Model 2 test set AUC score: 0.50
• Model 3 test set AUC score: 0.56
Applied Machine Learning in Python Module 3 Quiz Answer

 

• Model 1: Roc 1
• Model 2: Roc 2
• Model 3: Roc 3
• Model 1: Roc 1 
• Model 2: Roc 3
• Model 3: Roc 2
• Model 1: Roc 2
• Model 2: Roc 3
• Model 3: Roc 1
• Model 1: Roc 3
• Model 2: Roc 2
• Model 3: Roc 1
 
• Not enough information is given. 
 
 
Question 7) Given the following models and accuracy scores, match each model to its corresponding ROC curve.
 
• Model 1 test set accuracy: 0.91
• Model 2 test set accuracy: 0.79
• Model 3 test set accuracy: 0.72
 
Applied Machine Learning in Python Module 3 Quiz Answer

 

• Model 1: Roc 1
• Model 2: Roc 2
• Model 3: Roc 3
• Model 1: Roc 1
• Model 2: Roc 3
• Model 3: Roc 2
• Model 1: Roc 2
• Model 2: Roc 3
• Model 3: Roc 1
• Model 1: Roc 3
• Model 2: Roc 2
• Model 3: Roc 1

 

• Not enough information is given.

 

Question 8)
Using the fitted model `m` what is the micro precision score?
(Use y_test and X_test to compute the precision score.)
  1. #print(m)
  2. print(precision_score(y_test,m.predict(X_test),average=’micro’))
  • 0.744
Question 9)
Which of the following is true of the R-Squared metric? (Select all that apply)
  • The best possible score is 1.0
  • A model that always predicts the mean of y would get a negative score
  • A model that always predicts the mean of y would get a score of 0.0
  • The worst possible score is 0.0
Question 10)
In a future society, a machine is used to predict a crime before it occurs. If you were responsible for tuning this machine, what evaluation metric would you want to maximize to ensure no innocent people (people not about to commit a crime) are imprisoned (where crime is the positive label)?
  • Accuracy
  • Precision
  • Recall
  • F1
  • AUC
Question 11)
In a future society, a machine is used to predict a crime before it occurs. If you were responsible for tuning this machine, what evaluation metric would you want to maximize to ensure no innocent people (people not about to commit a crime) are imprisoned (where crime is the positive label)?
  • Accuracy
  • Precision
  • Recall
  • F1
  • AUC
Question 12)
A classifier is trained on an imbalanced multiclass dataset. After looking at the model’s precision scores, you find that the micro averaging is much smaller than the macro averaging score. Which of the following is most likely happening?
  • The model is probably misclassifying the frequent labels more than the infrequent labels.
  • The model is probably misclassifying the infrequent labels more than the frequent labels.
Question 13)
Using the already defined RBF SVC model `m`, run a grid search on the parameters C and gamma, for values [0.01, 0.1, 1, 10]. The grid search should find the model that best optimizes for recall. How much better is the recall of this model than the precision (Compute recall – precision to 3 decimal places)
 
(Use y_test and X_test to compute precision and recall.)
  1. #print(m) 
  2. parameters = {‘gamma’:[0.01, 0.1, 1, 10], ‘C’:[0.01, 0.1, 1, 10]} 
  3. clf = GridSearchCV(m,parameters,scoring=’recall’) 
  4. clf.fit(X_train,y_train) 
  5. y_pred = clf.best_estimator_.predict(X_test) 
  6. rec = recall_score(y_test, y_pred, average=’binary’) 
  7. pre = precision_score(y_test, y_pred, average=’binary’) 
  8. print(rec-pre)

 

  • 0.52 
 
Question 14)
Using the already defined RBF SVC model `m`, run a grid search on the parameters C and gamma, for values [0.01, 0.1, 1, 10]. The grid search should find the model that best optimizes for precision. How much better is the precision of this model than the recall? (Compute precision – recall to 3 decimal places)
(Use y_test and X_test to compute precision and recall.)
  1. #print(m)
  2. parameters = {‘gamma’:[0.01, 0.1, 1, 10], ‘C’:[0.01, 0.1, 1, 10]}
  3. clf = GridSearchCV(m,parameters,scoring=’precision’)
  4. clf.fit(X_train,y_train)
  5. y_pred = clf.best_estimator_.predict(X_test)
  6. rec = recall_score(y_test, y_pred, average=’binary’)
  7. pre = precision_score(y_test, y_pred, average=’binary’)
  8. print(pre-rec)
 
  • 0.15